「科学の方法と特徴(1)演繹法と帰納法」では、科学の方法として「演繹法」や「帰納法」、そしてこれらが合体した「仮説演繹法」というものがあることを紹介しました。

演繹法の問題についてはそこですでに触れましたので、今回は帰納法の問題から話を始めてみたいと思います。
ヒュームと帰納法

帰納法というのは「個別的な事例を観察して、そこから一般的な結論を導くこと」だと述べました。
100羽のカラスを観察したらみんな黒かったから、次に観察するカラスも黒いだろう。すべてのカラスは黒いはずだ……とか。
石を落とす実験を繰り返したら、石が落ちる距離はそれにかかる時間の2乗に比例した。いつもそうなった。だから次にやってもそうなるだろう。これは自然法則なのだ……とか。
つまり「何度やってもそうなるから、これは法則に違いない」という思考法がそこにはあるわけですね。
しかし、これに対して根本的な疑問を投げかけた哲学者がいます。懐疑主義者として有名なイギリスのヒュームです。18世紀に活躍した人です。
彼が問いかけたのは「なぜ、今までそうだったからという理由で、次もそうだと言えるのか?」ということです。
これが意外と難問でして、これに正面から反論できた哲学者や科学者は現在まで現れていないようです。
これまで「石の落ちる距離が時間の2乗に比例した」からと言って、どうして今後もそうだと言えるのか……
これに対して、普通なら「自然法則は一定に定まっているものだろう」と答えたくなります。
自然法則の秩序は不変であり(変わらないものであり)普遍である(どこでも成立するものである)から、帰納法によって繰り返し確認されたものは「法則」として確定してよいだろうというわけですね。
このように、自然秩序は一貫していて「同じ条件下なら同じ現象が起きる」という考え方を「自然の斉一性」と言います。
自然の斉一性(一様性とも言います)を前提すれば、確かに「繰り返し確認されたものは一般法則である」という帰納法は正しいことになるでしょう。
しかし議論がここで終わらずに、さらに「なんで自然の斉一性を前提していいの?」と言われたらハタと困ります。
これには「自然の斉一性はこれまでの科学が十分に示しているから」とか「これまで自然の斉一性を信じてうまくいってきたから」とか答えるしかありません。
すでにお気づきかもしれませんが、「これまでうまくいっていたから正しい」という考え方はこれ自体が1つの帰納法です。
つまり、自然の斉一性に基づいて帰納法を正当化したいのに、その自然の斉一性を帰納法で正当化しようとしているという「循環」が生じています。
したがって、純粋に論理学的に(あるいは哲学的に)考えるなら、「どうして帰納法を信用していいのか」という難問は解決できていないのです。
これは「帰納の正当化」問題と言われています。
ただ、帰納法がなければ科学も日常生活もままならないのですから、別にマニアックな科学哲学の世界で未解決でも放っておくしかないですよね(笑)
もしも「明日から突然に自然法則が変わる」という事態になったら、その時に慌てればいいでしょう。
帰納法をいかに正当化するかという問題については(グルーのパラドックスなど)他にもいくつかマニアックな議論がありますが、いかにも専門家の「思考遊び」のような感じなので触れなくてもいいでしょう。
理論負荷性と過少決定
個別の観察・実験から一般的な結論を導く帰納法には、もう少し現実的な問題もあります。
上で挙げたカラスのようなケースなら、誰がやってもそれほど結論はズレないと思われますが、もっと複雑で高度な現象になってくるとそうはいかなくなります。
実際には、観察や実験からデータが得られても、その科学者が事前にどんな理論を前提していたか(どんな背景知識を持っていたか)によって「データをどう解釈してどんな結論を導き出すか」が異なることがよくあるのです。
これを「理論負荷性」と言います。
この「観察は理論の影響を免れることはできない」という考え方は、20世紀のアメリカの科学哲学者であるハンソンが提唱しました。
理論負荷性については別の記事でも少しだけ触れました。同じ例で説明してみます。
↓↓↓↓↓↓↓↓↓↓↓↓
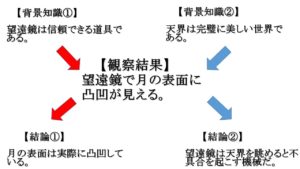
望遠鏡で月の表面を見ると凸凹が見えます。この「凸凹が見える」というのが実験結果ですね。
現代の僕たちなら、この実験結果から「月の表面は実際に凸凹している」と解釈し、そのことが証明されたと考えるでしょう。
しかし「月は完璧に美しい天体だ」という強い信念を持っている人が望遠鏡で月の凸凹を見ると、「望遠鏡は月に向けると正しく機能しない道具である」などとまったく別の解釈をしたりするのです(昔、実際にあった話です)。
↑↑↑↑↑↑↑↑↑↑↑↑
図にすると下のような感じです。
この例は極端に聞こえるかもしれませんが、理論負荷性は今後ますます重要になってくる概念だと思います。
現代科学は、人間が観測できない宇宙の始まりの様子とか、肉眼では観察できない素粒子の振る舞いとかについて、間接的な証拠に基づいて議論しています。
そうであるならば、「直接に観察できない世界についての解釈が、その科学者の持つ背景知識によってバラバラになってくる」という事態はこれまで以上に頻繁に起きるようになるのではないでしょうか。
もう1つ例を挙げます。
19世紀の後半、僕たちが普段から見ている「光」が「電磁波」という波の一種であることが分かりました。
それを聞いたある人々は「エーテルの存在が証明された」と解釈したのです。
この場合の「エーテル」とは光を伝えるための媒質として想定されていた物質です(エーテルというのはたくさん意味があるので要注意)。
当時は「波が伝わるには必ずそのための媒質が要る」という理論を持つ人たちがいました。水面で波が伝わっていくためには水という媒質が要るのと同じです。
だから、光が電磁波という波の一種であることが分かったとき、そのことと同時に光を伝える媒質である「エーテル」の存在も証明されたと解釈したわけです。
しかし「波が伝わるには必ず媒質が要る」という理論を前提していない人たちにとっては、「光は電磁波という波である」から「光の媒質であるエーテルが存在する」は出てきません。
これは理論負荷性を示す実例ですが、こうした例は科学史からいくらでも挙げられるでしょう。
ちなみに、この「実験結果は1つでも、背景にある理論によって解釈が複数に分かれることがある」という理論負荷性を反対側から言うと、「実験によっては複数の理論の間の優劣を判定できないことがある」ということになるでしょう。
このことを「過小決定」あるいは「決定不全」と呼びます。
さて以上、いろいろと述べてきました。
帰納法は実験や観察を通して「個別の事例から一般的な結論を導く」という方法ですが、単純に「実験や観察をしていればオールオッケー」というわけではないことが分かります。
とは言え、実験や観察を重ねることで(結論を1つに絞り込めないことも多いのですが)明らかに不合理な理論は徐々に排除され、正しい解釈の範囲が狭まることで、真理に近づいてゆくことが可能になるでしょう。
科学の「全体論」(ホーリズム)
せっかくいくつかの事例を出しましたので、これらに関連する話題を1つご紹介して終わりにしたいと思います。
例えば月の表面が実際に凸凹しているかを観察する場合、望遠鏡で月を眺めてみればそれでいいわけではありません。
なぜなら「天界は完璧に美しい世界である」「天体の観察をすると望遠鏡は不具合を起こす」などと主張する人たちがいるからです。
したがって、「望遠鏡はどういう仕組みになっているのか」「どうして地上だけでなく天界も正しく映し出す道具であると言っていいのか」といった理論も関係してきます。
あるいは「天界は完璧に美しい世界だ」という理論にどういった根拠があるのか。それを裏付けるような証拠、逆にそれを反駁するような証拠はあるのか……等々、これについても考慮しなければいけないでしょう。
要するに、「月の表面が実際に凸凹している」という見解を単独で取り出してきて、それを実験や観察によって検証するということは難しいのです。
これを検証しようとするなら、これに関係する多くの理論を考慮に入れた上でやる必要があるわけですね。
科学における1つの見解というのは、それ以外の様々な理論や証拠と論理的に(演繹的に)つながっているからです。
科学の理論というのは、個々別々になっているのではなく、全体が体系(システム)として1つにつながっています。こういう考えを「ホーリズム」(全体論)と言います。
政治の「全体主義」(トータリタリアニズム)とは違うのでご注意を。
このホーリズムという概念を提示したのは、20世紀のアメリカの哲学者・論理学者であるクワインという人です。
それ以前にほぼ同じことを言っていたフランスの科学哲学者にデュエムという人もいます。ですので、ホーリズムはこの2人の名前をとって「デュエム=クワイン・テーゼ」と呼ばれることもあります。
「この2人の主張は微妙に違う」として研究している専門家の方もいますが、細かい話ですし、僕も聞いてもよく分からないので別にいいでしょう(^^;)。
もちろん、「これについては単独で検証できているのではないか」というものもあって、ホーリズムがあらゆるケースに当てはまるかどうかは分かりません。議論は続いているようです。
しかし一般論としては、「科学理論はシステムとして結びついていて切り離しが難しい」「実験・観察によって一発で検証できるわけではない」というのはその通りでしょう。
その意味で科学の特徴をよくとらえた概念であると言えるでしょう。
次回「科学の方法と特徴(3)科学のパラダイムシフト」では、「パラダイム」という概念を用いながら「科学はいかにして発展していくのか」という議論を紹介します。


